[TOC]
Overview
滑动窗口与共视图
我们根据 时空 对 局部BA 进行分类:
- 时间:滑动窗口
- 空间:共视图
通过 企业管理,解释滑窗的边缘化以及共视图为啥没有边缘化:
基于滑窗优化的边缘化,可以用公司小组成员离职类比,小组相当于滑窗,离职交接相当于保留共视信息,没有交接就回影响小组未来的发展;交接不好,重新搞;员工贡献不大直街裁掉,就是remove或throw;而基于共视图的,相当于组长从他的人脉网招人搭建队伍做事。
Eliminate Old Variables
Marginal Probability
\[\begin{aligned} P(\boldsymbol{a}, \boldsymbol{b}) &=\mathcal{N}\left(\left[\begin{array}{l} \boldsymbol{\mu}_{a} \\ \boldsymbol{\mu}_{b} \end{array}\right],\left[\begin{array}{ll} \boldsymbol{\Sigma}_{a a} & \boldsymbol{\Sigma}_{a b} \\ \boldsymbol{\Sigma}_{b a} & \boldsymbol{\Sigma}_{b b} \end{array}\right]\right) \\ &=\mathcal{N}^{-1}\left(\left[\begin{array}{l} \boldsymbol{\eta}_{a} \\ \boldsymbol{\eta}_{b} \end{array}\right],\left[\begin{array}{cc} \boldsymbol{\Lambda}_{a a} & \boldsymbol{\Lambda}_{a b} \\ \boldsymbol{\Lambda}_{b a} & \boldsymbol{\Lambda}_{b b} \end{array}\right]\right) \end{aligned}\]Marginalization and Conditioning operations on a gaussian distribution expresssed in convariance and information form.
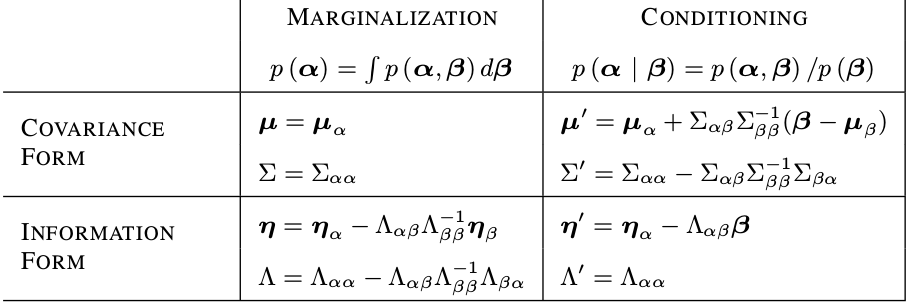
Three Math Methods for Marginalization
-
Throwing Rows and Cols with Covariance Matrix (Filter-based)
-
Nullspace Projection with Jacobian Matrix (MSCKF)
- SVD
- QR
-
Schur Complement with Hessian/Information Matrix (Optimization-based Sliding window)
舒尔补 (Schur Complement)
\[M= \left[\begin{array}{ll} A & B \\ C & D \end{array}\right]\]则 D在M中的舒尔补 为
\[M / D := A-B D^{-1} C\]在矩阵方程求解中的应用
线性方程组
\[\begin{aligned} &A x+B y=a \\ &C x+D y=b \end{aligned}\]利用 D的舒尔补 先求 $x$
\[\left(A-B D^{-1} C\right) x=a-B D^{-1} b\]解出未知量 $x$ 之后带入第二个方程 $C x+D y=b$ 就可以解出 $y$
Marginalization in VINS-Mono
Two way marginalization
- 当滑动窗口中第二新的图像帧为关键帧,则 marg 最老的帧,以及上面的路标点;
- 当滑动窗口中第二新的图像帧不是关键帧,则丢弃这一帧上的视觉测量信息,IMU 预积分传给下一帧。
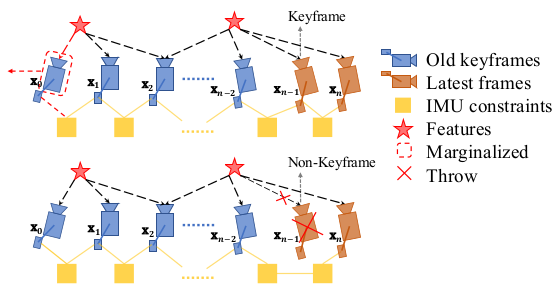
数据结构
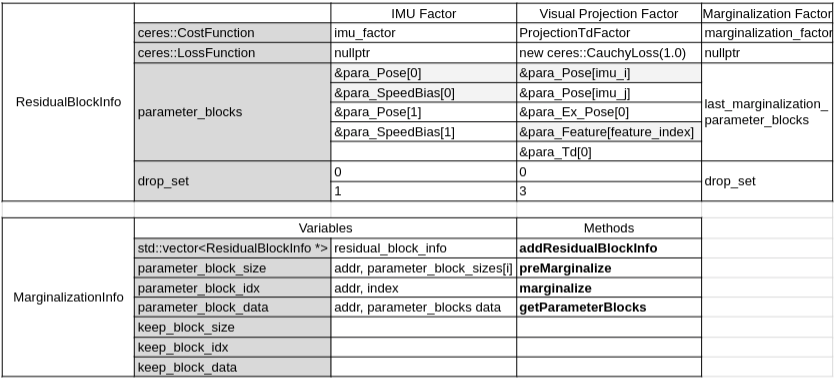
代码逻辑
addResidualBlockInfo
factors.emplace_back(residual_block_info);
std::vector<int> &drop_set = residual_block_info->drop_set;
std::vector<double *> ¶meter_blocks = residual_block_info->parameter_blocks;
for (int i = 0; i < parameter_blocks.size(); i++) {
long addr = reinterpret_cast<long>(parameter_blocks[i]);
parameter_block_size[addr] =
residual_block_info->cost_function->parameter_block_sizes()[i];
}
for (int i = 0; i < drop_set.size(); i++) {
long addr = reinterpret_cast<long>(parameter_blocks[drop_set[i]]);
parameter_block_idx[addr] = 0;
}
preMarginalize
for (auto it : factors) {
it->Evaluate(); // 利用多态性分别计算所有状态变量构成的残差和雅克比矩阵
std::vector<int> block_sizes = it->cost_function->parameter_block_sizes();
for (int i = 0; i < static_cast<int>(block_sizes.size()); i++) {
int size = block_sizes[i];
long addr = reinterpret_cast<long>(it->parameter_blocks[i]);
if (parameter_block_data.find(addr) == parameter_block_data.end()) {
double \*data = new double[size];
memcpy(data, it->parameter_blocks[i], sizeof(double) * size);
parameter_block_data[addr] = data;
}
}
}
marginalize
Marginalization via Schur complement on information matrix
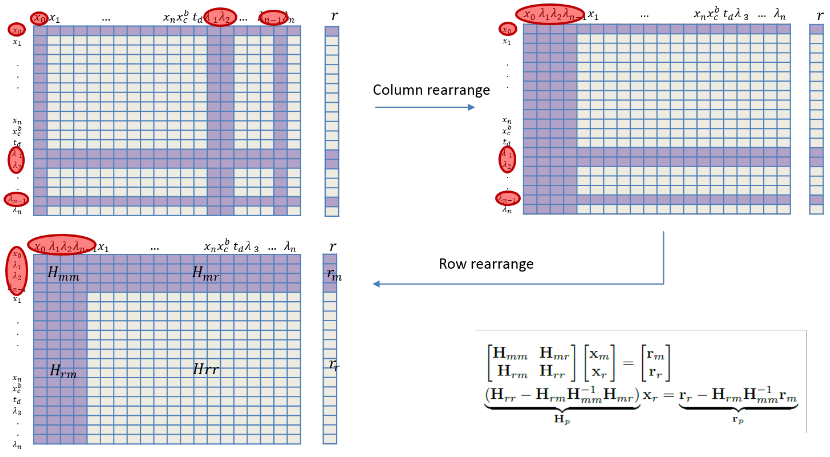
fill in of the information matrix
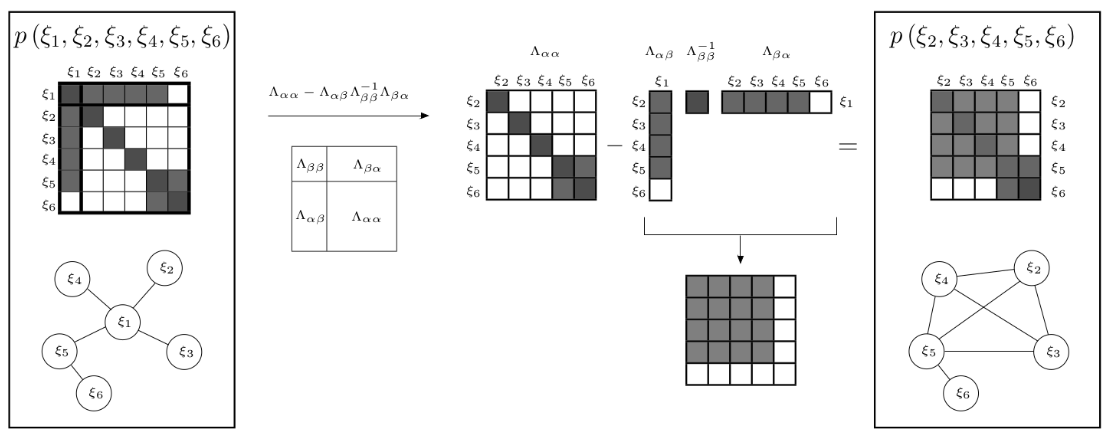
linearized_jacobians & linearized_residuals

A = Arr - Arm * Amm_inv * Amr;
b = brr - Arm * Amm_inv * bmm;
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);
Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));
Eigen::VectorXd S_sqrt = S.cwiseSqrt();
Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;
MarginalizationFactor::Evaluate

int n = marginalization_info->n;
int m = marginalization_info->m;
Eigen::VectorXd dx(n);
for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++) {
int size = marginalization_info->keep_block_size[i];
int idx = marginalization_info->keep_block_idx[i] - m;
Eigen::VectorXd x = Eigen::Map<const Eigen::VectorXd>(parameters[i], size);
Eigen::VectorXd x0 = Eigen::Map<const Eigen::VectorXd>(marginalization_info->keep_block_data[i], size);
if (size != 7)
dx.segment(idx, size) = x - x0;
else {
Eigen::Quaterniond q_tmp =
Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5));
dx.segment<3>(idx + 0) = x.head<3>() - x0.head<3>();
dx.segment<3>(idx + 3) = 2.0 * Utility::positify(q_tmp).vec();
if (!(q_tmp.w() >= 0)) {
dx.segment<3>(idx + 3) = 2.0 * -Utility::positify(q_tmp).vec();
}
}
}
Eigen::Map<Eigen::VectorXd>(residuals, n) =
marginalization_info->linearized_residuals + marginalization_info->linearized_jacobians * dx;
if (jacobians) {
for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++) {
if (jacobians[i]) {
int size = marginalization_info->keep_block_size[i];
int local_size = marginalization_info->localSize(size);
int idx = marginalization_info->keep_block_idx[i] - m;
Eigen::Map<Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> jacobian(jacobians[i], n, size);
jacobian.setZero();
jacobian.leftCols(local_size) = marginalization_info->linearized_jacobians.middleCols(idx, local_size);
}
}
}
Add New Variables
Consistency in SW
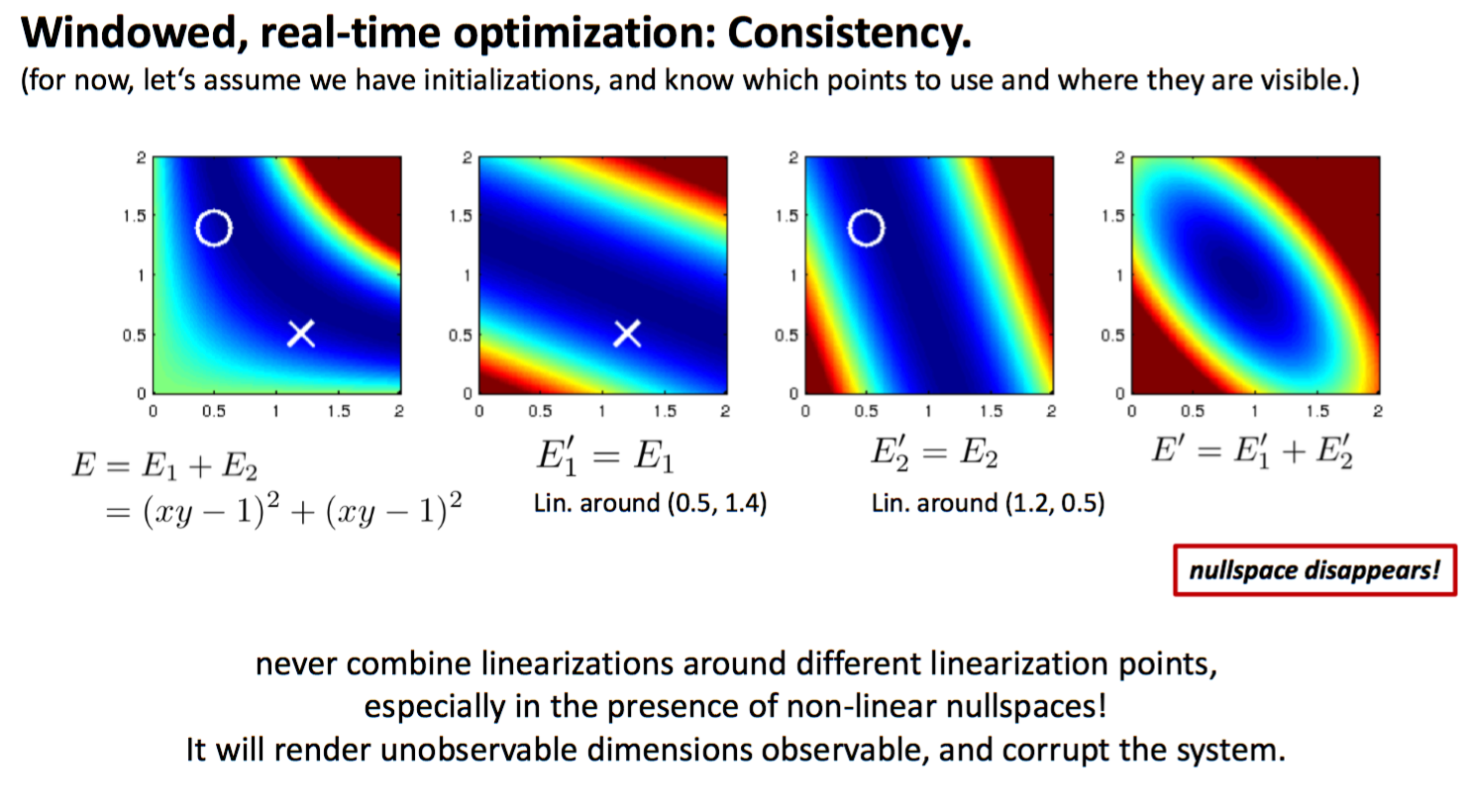
多个解的问题,变成了一个确定解。不可观的变量,变成了可观的。
边缘化后增加新变量
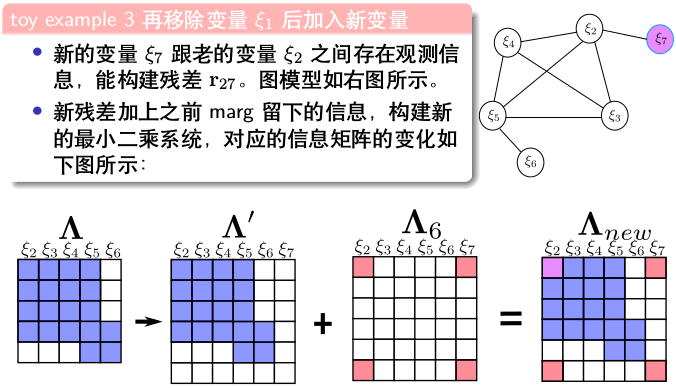
注意: $\xi_2$ 自身的信息矩阵由两部分组成,这会使得系统存在潜在风险。
滑动窗口中的问题:滑动窗口算法中,对于同一个变量,不同残差对其计算雅克比矩阵时线性化点可能不一致,导致信息矩阵可以分成两部分,相当于在信息矩阵中多加了一些信息,使得其零空间出现了变化。

解决办法:First Estimated Jacobian。
First Estimate Jacobian (FEJ)
FEJ 算法:不同残差对同一个状态求雅克比时,线性化点必须一致,这样就能避免零空间退化而使得不可观变量变得可观。