Overview 1
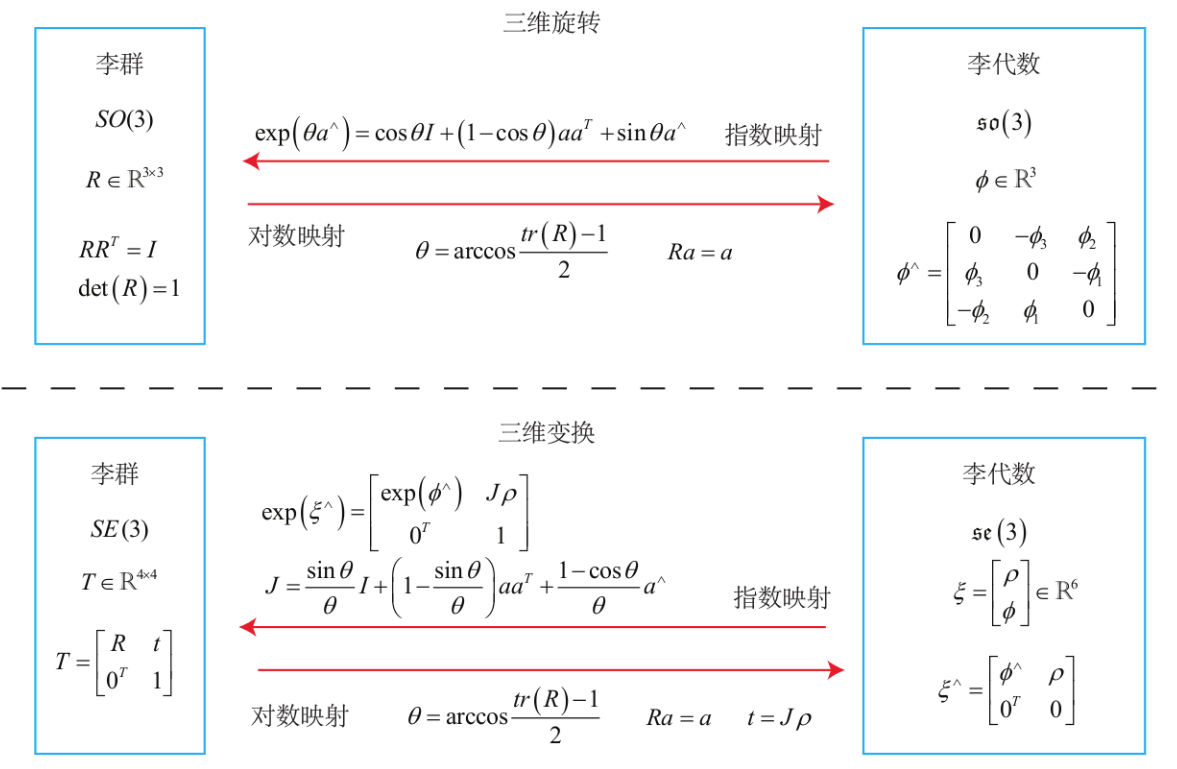
Matrix Exponential & Logarithm
已知 $A \in \mathbb{R}^{M \times M}$,
\[\exp (\mathbf{A}) =\sum_{n=0}^{\infty} \frac{1}{n !} \mathbf{A}^{n} =\mathbf{1}+\mathbf{A}+\frac{1}{2 !} \mathbf{A}^{2}+\frac{1}{3 !} \mathbf{A}^{3}+\cdots\] \[\ln (\mathbf{A})=\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n}(\mathbf{A}-\mathbf{1})^{n}\]Lie Bracket
TODO
$SU(2)$ and the Quaternions 2
\[R = C(q) \longrightarrow R^T = C(q^{-1})\]欧拉公式
\[e^{ix} = \cos x + i \sin x\]

2D旋转
单位复数 可用来表示2D旋转。
\[z = a + b\vec{i} = r (\cos \theta + \sin \theta \vec{i} ) = e^{\theta \vec{i}}, \quad r = ||z||=1\]3D旋转
单位四元数 才可表示3D旋转,四元数是复数的扩充,在表示旋转前需要进行 归一化。
\[\mathbf{q} = \exp(\frac{\boldsymbol \phi}{2}) = \exp \left( \frac{\mathbf{u} \theta}{2} \right) = \cos \frac{\theta}{2} + \mathbf{u} \sin \frac{\theta}{2} = \begin{bmatrix} \cos \frac{\theta}{2} \\ \mathbf{u} \sin \frac{\theta}{2} \end{bmatrix} \quad s.t. \quad ||\mathbf{q}||_2 = 1\]当 $\theta$ 很小时,一阶泰勒展开,可以近似表达为
\[\mathbf{q} = \exp({\frac{\mathbf{u}\theta}{2}}) \approx 1 + \frac{\mathbf{u}\theta}{2} = \begin{bmatrix} 1 \\ \frac{\mathbf{u}\theta}{2} \end{bmatrix} = \begin{bmatrix} 1 \\ \frac{\boldsymbol{\phi}}{2} \end{bmatrix}\]四元数可以在 保证效率 的同时,减小矩阵1/4的内存占有量,同时又能 避免欧拉角的万向锁问题。
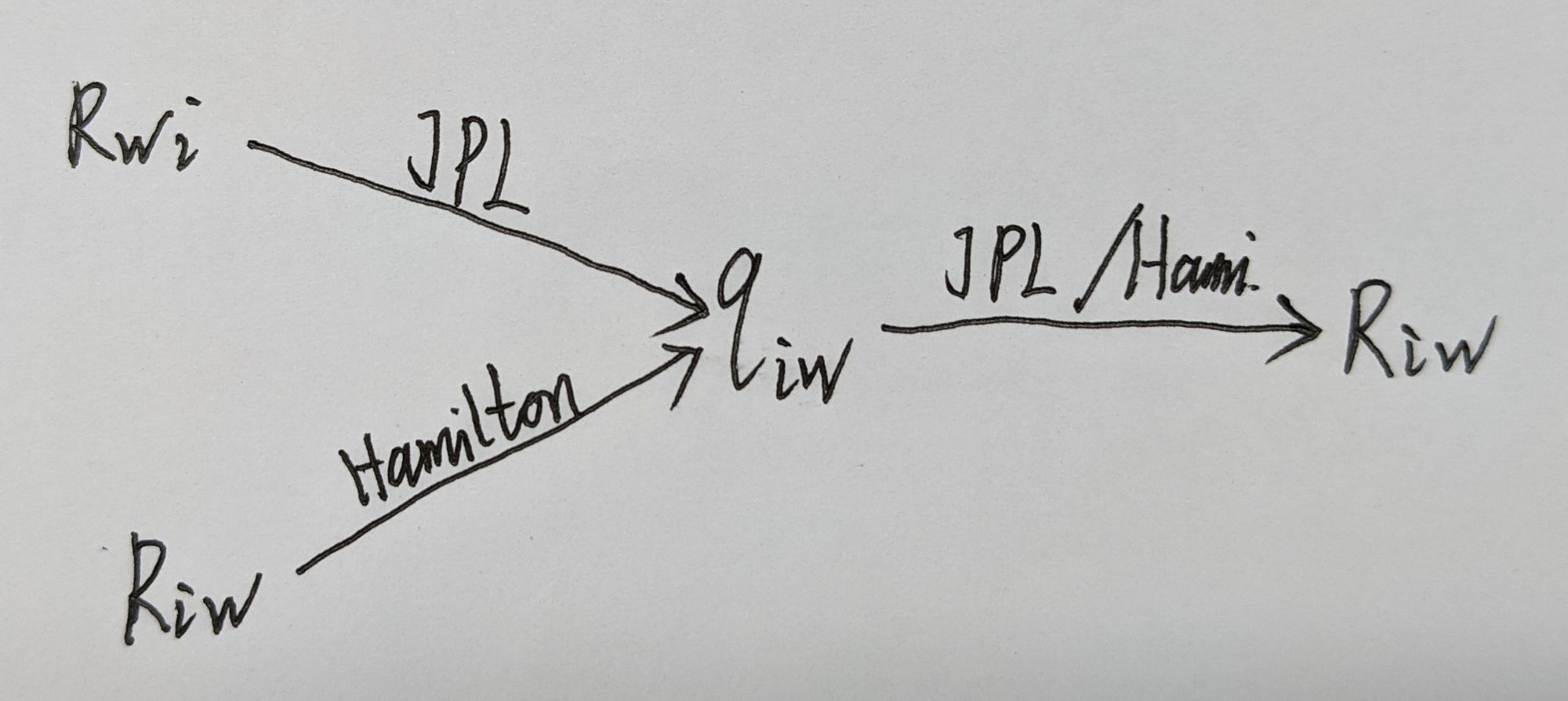
Hamilton & JPL 四元数
$SO(3)$
Lie Group $SO(3)$
\[SO(3) = \Bigg\{ \mathbf{R} \in \mathbb{R}^{3 \times 3} \Bigg| \mathbf{RR}^T = \mathbf{I}, det(\mathbf{R}) = 1 \Bigg\}\]Lie Algebra $\mathfrak{so}(3)$
\[\mathfrak{so}(3) = \Bigg\{ \boldsymbol{\Phi} = \boldsymbol{\phi}^{\wedge} \in \mathbb{R}^{3 \times 3} \Bigg| \boldsymbol{\phi} \in \mathbb{R}^3 \Bigg\}\]where
\[\boldsymbol{\phi}^{\wedge} = \begin{bmatrix} \phi_1 \\ \phi_2 \\ \phi_3 \end{bmatrix}^{\wedge} = \begin{bmatrix} 0 & -\phi_3 & \phi_2 \\ \phi_3 & 0 & -\phi_1 \\ -\phi_2 & \phi_1 & 0 \end{bmatrix} \in \mathbb{R}^{3 \times 3}\]Infinitesimal Rotations
the base of $\mathfrak{so}(3)$ are three skew symmetric matrices, each corresponding to infinitesimal rotations along each axis
\[\mathbf{G}_{1}^{\mathfrak{s o}(3)}=\mathbf{e}_{1}^{\wedge}=\left(\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{array}\right) \quad \mathbf{e}_{1}=\left[\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right]\] \[\mathbf{G}_{2}^{\mathfrak{s o}(\mathbf{3})}=\mathbf{e}_{2}^{\wedge}=\left(\begin{array}{ccc} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{array}\right) \quad \mathbf{e}_{2}=\left[\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right]\] \[\mathbf{G}_{3}^{\mathfrak{s o}(3)}=\mathbf{e}_{3}^{\wedge}=\left(\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right) \quad \mathbf{e}_{3}=\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right]\]then the $\mathfrak{so}$(3)
\[\mathfrak{s o}(3)=\left\{\mathbf{G}_{\mathbf{i}}^{\mathfrak{s o}(\mathbf{3})}\right\}_{i=1,2,3}\]映射
指数映射
\[\begin{aligned} \mathbf{R} &= \exp(\boldsymbol{\phi}^{\wedge}) \\ &= \mathbf{I} + \boldsymbol{\phi}^{\wedge} \mathbf{J}_l \quad \text{???} \end{aligned}\]当 $|\phi|$ 比较小时,一阶泰勒近似
\[\mathbf{R} \approx \mathbf{I} + \boldsymbol{\phi}^{\wedge}\]对数映射
\[\boldsymbol{\phi} = \log(\mathbf{R})^{\vee}\]$SE(3)$
Lie Group $SE(3)$
\[SE(3) = \Bigg\{ \mathbf{T} = \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{bmatrix} \in \mathbb{R}^{4 \times 4} \Bigg| \mathbf{R} \in SO(3), \mathbf{t} \in \mathbb{R}^{3} \Bigg\}\]Lie Algebra $\mathfrak{se}(3)$
\[\mathfrak{se}(3) = \Bigg\{ \boldsymbol{\Xi} = \boldsymbol{\xi}^{\wedge} \in \mathbb{R}^{4 \times 4} \Bigg| \boldsymbol{\xi} \in \mathbb{R}^6 \Bigg\}\]where
\[\boldsymbol{\xi}^{\wedge} = \begin{bmatrix} \boldsymbol{\rho} \\ \boldsymbol{\phi} \end{bmatrix}^{\wedge} = \begin{bmatrix} \boldsymbol{\phi}^{\wedge} & \boldsymbol{\rho} \\ \mathbf{0}^T, & 0 \end{bmatrix} \in \mathbb{R}^{4 \times 4}, \quad \boldsymbol{\rho},\boldsymbol{\phi} \in \mathbb{R}^3\]The infinitesimal generators of SE(3)
the base of $\mathfrak{se}(3)$ are these six 4×4 matrices, each corresponding to either infinitesimal rotations or infinitesimal translations along each axis
\[\mathbf{G}_{\{\mathbf{1 , 2 , 3}\}}^{\mathfrak{s e}(3)} =\left(\begin{array}{c|c} & 0 \\ \mathbf{G}_{\{\mathbf{1}, \mathbf{2}, \mathbf{3}\}}^{\mathfrak{s o}(3)} & 0 \\ & 0 \\ \hline 0 & 0 \end{array}\right)\] \[\mathbf{G}_{4}^{\mathfrak{s c}(3)} =\left(\begin{array}{c|c} & 1 \\ \mathbf{0}_{3 \times 3} & 0 \\ & 0 \\ \hline 0 & 0 \end{array}\right) \quad \quad \mathbf{G}_{5}^{\mathfrak{s c}(3)}=\left(\begin{array}{c|c} & 0 \\ \mathbf{0}_{3 \times 3} & 1 \\ & 0 \\ \hline 0 & 0 \end{array}\right) \quad \quad \mathbf{G}_{6}^{\mathfrak{s c}(3)}=\left(\begin{array}{c|c} & 0 \\ \mathbf{0}_{3 \times 3} & 0 \\ & 1 \\ \hline 0 & 0 \end{array}\right)\]then the $\mathfrak{se}(3)$
\[\mathfrak{s e}(3)=\left\{\mathbf{G}_{\mathbf{i}}^{\mathfrak{s e}(3)}\right\}_{i=1 \ldots 6}\]so
\[\xi^\wedge = \sum_{i=1}^6 \xi(i) \cdot G_i\]Sophus::Matrix4d sk_b1;
sk_b1.setZero();
for (int i = 0; i < vec_b.size(); i++) {
sk_b1 += vec_b[i] * Sophus::SE3d::generator(i);
}
Jacobian
to convert the translation component of pose in $\mathfrak{se}(3)$ into the translation component of pose in $SE(3)$ through
\[\mathbf{t}=\mathbf{J}_l \boldsymbol{\rho} \in \mathbb{R}^{3}, \quad \mathbf{J}_l=\sum_{n=0}^{\infty} \frac{1}{(n+1) !}\left(\phi^{\wedge}\right)^{n}\]映射
指数映射
\[\mathbf{T} = \exp(\boldsymbol{\xi}^{\wedge})\]对数映射
\[\boldsymbol{\xi} = \log(\mathbf{T})^{\vee}\]Adjoints
Adjoint action of SE(3)
- https://gtsam.org/2021/02/23/uncertainties-part3.html
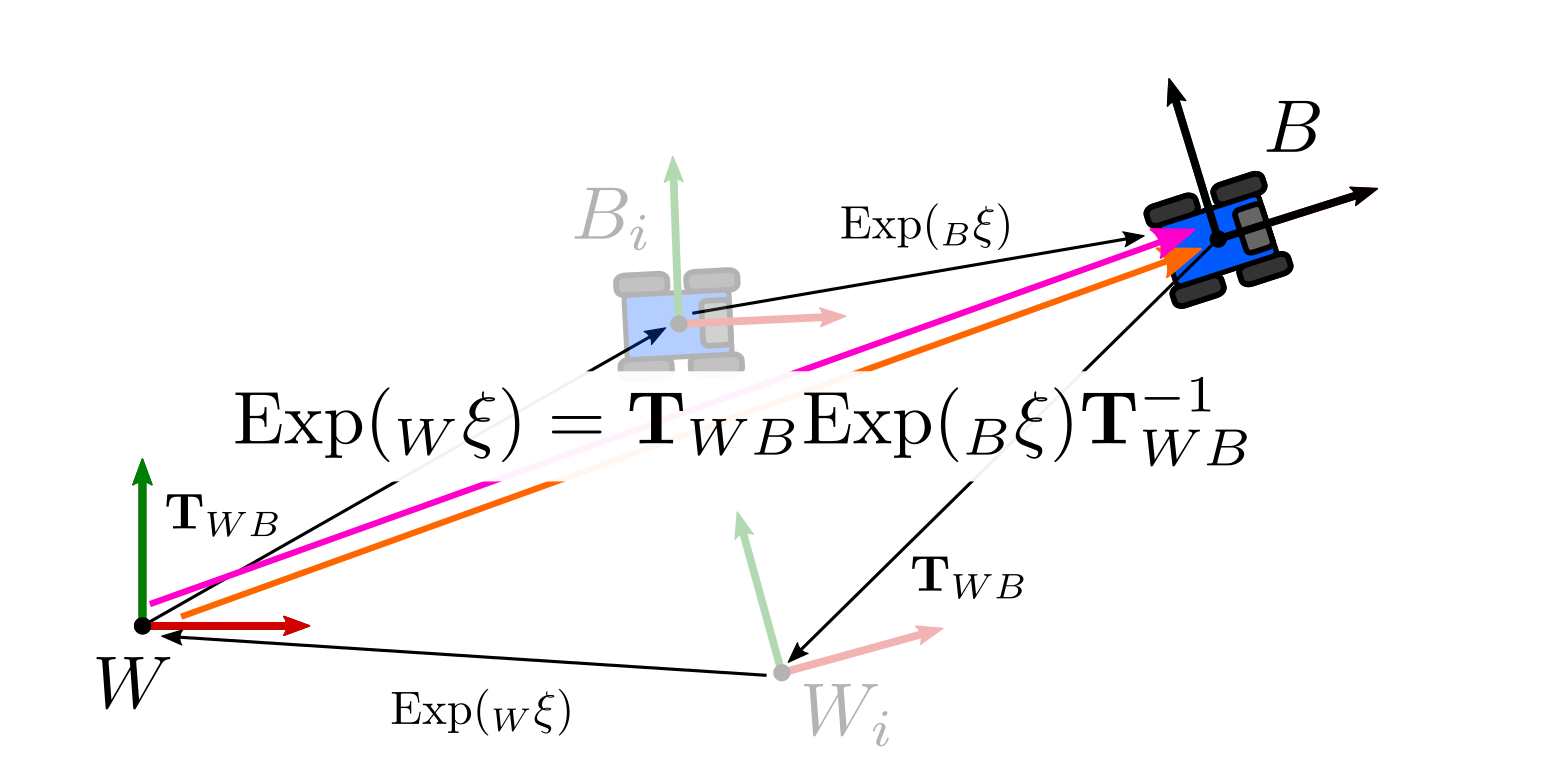
上图用伴随表示:
\[\exp(\xi_w^{\wedge}) = T_{wb} \cdot \exp(\xi_b^{\wedge}) \cdot T_{wb}^{-1} = \exp((\mathtt{Adj}_{T_{wb}} \cdot \xi_b)^{\wedge})\]with the key property of exponential map
\[\exp(T \xi^\wedge T^{-1}) = T \cdot \exp(\xi^\wedge) \cdot T^{-1}\]we can get
\[T \xi^\wedge T^{-1} = (\mathtt{Adj}_{T} \cdot \xi)^{\wedge}\]so, for $SO(3)$
\[R \phi^{\wedge} R^T = (R \phi)^{\wedge}\]同一刚体中不同坐标系姿态变换的相互表示
以带有IMU的相机模组为例,已知 IMU(坐标系)本身的姿态变换 $\mathbf{T}^{B}$ 和 同一模组中Camera到IMU(Body)的坐标系变换 $\mathbf{T}_{BC}$,则 该Camera(坐标系)本身的姿态变换为:
\[{}_C\mathbf{T} = \mathbf{T}_{BC} \cdot \mathbf{T}^{B} \cdot \mathbf{T}_{BC}^{-1}\]因为上面的变换都是 坐标系的变换,所以矩阵相乘 从左到右,即 矩阵右乘

Exponential Map on $SE(3)$
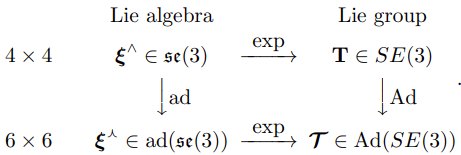
Eigen::Matrix3d R_b = Eigen::AngleAxisd(M_PI / 4, Eigen::Vector3d(0, 1, 0)).toRotationMatrix();
Sophus::SO3d SO3_b(R_b);
Sophus::SE3d::Tangent vec_b;
vec_b.head(3) << 10.1793, -6.3204, 28.09113;
vec_b.tail(3) = SO3_b.log();
Sophus::Vector3d t_wb(1.2, 3.4, 5.6);
Sophus::SE3d SE3_wb(R, t_wb);
Sophus::SE3d SE3_w = SE3_wb * Sophus::SE3d::exp(vec_b) * SE3_wb.inverse();
Sophus::SE3d::Tangent vec_w0 = SE3_w.log();
Sophus::SE3d::Tangent vec_w1 = Sophus::SE3d::vee(SE3_wb.matrix() * Sophus::SE3d::hat(vec_b) * SE3_wb.inverse().matrix());
Sophus::SE3d::Tangent vec_w2 = Sophus::SE3d::exp(vec_w1).log();
Sophus::SE3d::Tangent vec_b_adj = SE3_wb.Adj() * vec_b;
std::cout << "vec_w0 :" << vec_w0.transpose() << std::endl;
std::cout << "vec_w1 :" << vec_w1.transpose() << std::endl;
std::cout << "vec_w2 :" << vec_w2.transpose() << std::endl;
std::cout << "vec_b_adj :" << vec_b_adj.transpose() << std::endl;
output:
vec_w0 : 6.3204 5.78107 30.7615 -0.785398 1.13928e-16 0
vec_w1 : 6.3204 5.78107 30.7615 -0.785398 1.74393e-16 0
vec_w2 : 6.3204 5.78107 30.7615 -0.785398 1.74393e-16 0
vec_b_adj : 6.3204 5.78107 30.7615 -0.785398 1.74393e-16 0
Baker-Campbell-Hausdorff (BCH)
Properties
\[\exp((\phi + \delta \phi)^{\wedge}) \approx \exp((J_l \delta \phi)^{\wedge}) \cdot \exp({\phi}^{\wedge}) = \exp((J_l \delta \phi)^{\wedge}) \cdot R\] \[\exp((\phi + \delta \phi)^{\wedge}) \approx \exp({\phi}^{\wedge}) \cdot \exp((J_r \delta \phi)^{\wedge}) = R \cdot \exp((J_r \delta \phi)^{\wedge})\]where
\[J_l = J_l (\phi), \quad J_r = J_r (\phi)\]and
\[\boldsymbol{J}_{l}=\boldsymbol{J}=\frac{\sin \phi}{\phi} \boldsymbol{I}+\left(1-\frac{\sin \phi}{\phi}\right) \boldsymbol{a} \boldsymbol{a}^{T}+\frac{1-\cos \phi}{\phi} \boldsymbol{a}^{\wedge}\] \[\boldsymbol{J}_{r}=\boldsymbol{J}=\frac{\sin \phi}{\phi} \boldsymbol{I}+\left(1-\frac{\sin \phi}{\phi}\right) \boldsymbol{a} \boldsymbol{a}^{T}-\frac{1-\cos \phi}{\phi} \boldsymbol{a}^{\wedge}\]so
\[J_l (-\phi) = J_r (\phi)\]当 $\phi$ 很小时
\[J_l \approx I, \quad J_r \approx I\]Rotations
The BCH formula
\[\begin{aligned} \ln \left(\mathbf{C}_{1} \mathbf{C}_{2}\right)^{\vee}=\ln (\exp (&\left.\left.\phi_{1}^{\wedge}\right) \exp \left(\phi_{2}^{\wedge}\right)\right)^{\vee} \\ & \approx\left\{\begin{array}{ll} \mathbf{J}_{\ell}\left(\phi_{2}\right)^{-1} \phi_{1}+\phi_{2} & \text { if } \phi_{1} \text { small } \\ \phi_{1}+\mathbf{J}_{r}\left(\phi_{1}\right)^{-1} \phi_{2} & \text { if } \phi_{2} \text { small } \end{array},\right. \end{aligned}\]In Lie group theory, $J_r$ and $J_l$ are referred to as the right and left Jacobians of $SO(3)$, respectively.
Libs
- Sophus
- manif: A small header-only library for Lie theory