On-Manifold Optimization: Local Parameterization

Overview

Manifold Space vs Tangent Space

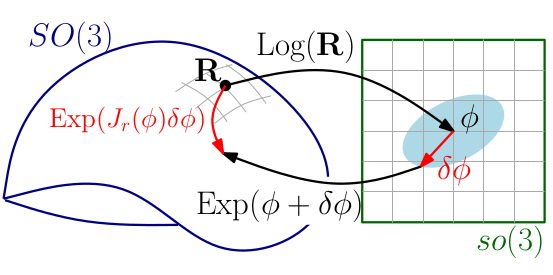
Jacobian w.r.t Error State

Jacobian w.r.t Error State vs True State

According ¹ 2.4,

The idea is that for a $x \in N$ the function $g(\delta) := f (x \boxplus \delta)$ behaves locally in $0$ like $f$ does in $x$. In particular $|f(x)|^2$ has a minimum in $x$ if and only if $|g(\delta)|^2$ has a minimum in $0$. Therefore finding a local optimum of $g$, $\delta = \arg \min_{\delta} |g(\delta)|^2$ implies $x \boxplus \delta = \arg \min_{\xi} |f(\xi)|^2$.

\[f(x \boxplus \delta)=f(x)+J_x \delta+\mathcal{O}\left(\|\delta\|^2\right)\]

where

\[J = \left. \frac{\partial f(x \boxplus \delta)}{\partial \delta} \right|_{\delta=0} \quad \longleftrightarrow \quad J = \left. \frac{\partial f(x)}{\partial x} \right|_{x}\]

ESKF ² 6.1.1: Jacobian computation

\[\left.\mathbf{H} \triangleq \frac{\partial h}{\partial \delta \mathbf{x}}\right|_{\mathbf{x}}=\left.\left.\frac{\partial h}{\partial \mathbf{x}_t}\right|_{\mathbf{x}} \frac{\partial \mathbf{x}_t}{\partial \delta \mathbf{x}}\right|_{\mathbf{x}}=\mathbf{H}_{\mathbf{x}} \mathbf{X}_{\delta \mathbf{x}}\]

$x_t$: true state
$x$: normal state
$\delta x$: error state

lifting and retraction:

\[\left.\mathbf{X}_{\delta \mathbf{x}} \triangleq \frac{\partial \mathbf{x}_t}{\partial \delta \mathbf{x}}\right|_{\mathbf{x}}=\left[\begin{array}{ccc} \mathbf{I}_6 & 0 & 0 \\ 0 & \mathbf{Q}_{\delta \boldsymbol{\theta}} & 0 \\ 0 & 0 & \mathbf{I}_9 \end{array}\right]\]

the quaternion term

\[\begin{aligned} \left.\mathbf{Q}_{\delta \boldsymbol{\theta}} \triangleq \frac{\partial(\mathbf{q} \otimes \delta \mathbf{q})}{\partial \delta \boldsymbol{\theta}}\right|_{\mathbf{q}} &=\left.\left.\frac{\partial(\mathbf{q} \otimes \delta \mathbf{q})}{\partial \delta \mathbf{q}}\right|_{\mathbf{q}} \frac{\partial \delta \mathbf{q}}{\partial \delta \boldsymbol{\theta}}\right|_{\delta \hat{\boldsymbol{\theta}}=0} \\ &=\left.\left.\frac{\partial\left([\mathbf{q}]_L \delta \mathbf{q}\right)}{\partial \delta \mathbf{q}}\right|_{\mathbf{q}} \frac{\partial\left[\begin{array}{c} 1 \\ \frac{1}{2} \delta \boldsymbol{\theta} \end{array}\right]}{\partial \delta \boldsymbol{\theta}}\right|_{\hat{\delta}=0} \\ &=[\mathbf{q}]_L \frac{1}{2}\left[\begin{array}{lll} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \end{aligned}\]

Least Squares on a Manifold ³

Local Parameterization in Ceres Solver ⁴ ⁵ ⁶ ⁷ ⁸

class LocalParameterization {
 public:
  virtual ~LocalParameterization() = default;
  virtual bool Plus(const double* x,
                    const double* delta,
                    double* x_plus_delta) const = 0;
  virtual bool ComputeJacobian(const double* x, double* jacobian) const = 0;
  virtual bool MultiplyByJacobian(const double* x,
                                  const int num_rows,
                                  const double* global_matrix,
                                  double* local_matrix) const;
  virtual int GlobalSize() const = 0;
  virtual int LocalSize() const = 0;
};

Plus

Retraction

\[\boxplus(x, \Delta)=x \operatorname{Exp}(\Delta)\]

ComputeJacobian

global w.r.t local

\[J_{GL} = \frac{\partial x_G}{\partial x_L} = D_2 \boxplus(x, 0) = \left. \frac{\partial \boxplus(x, \Delta)}{\partial \Delta} \right|_{\Delta = 0}\]

参考 ⁹

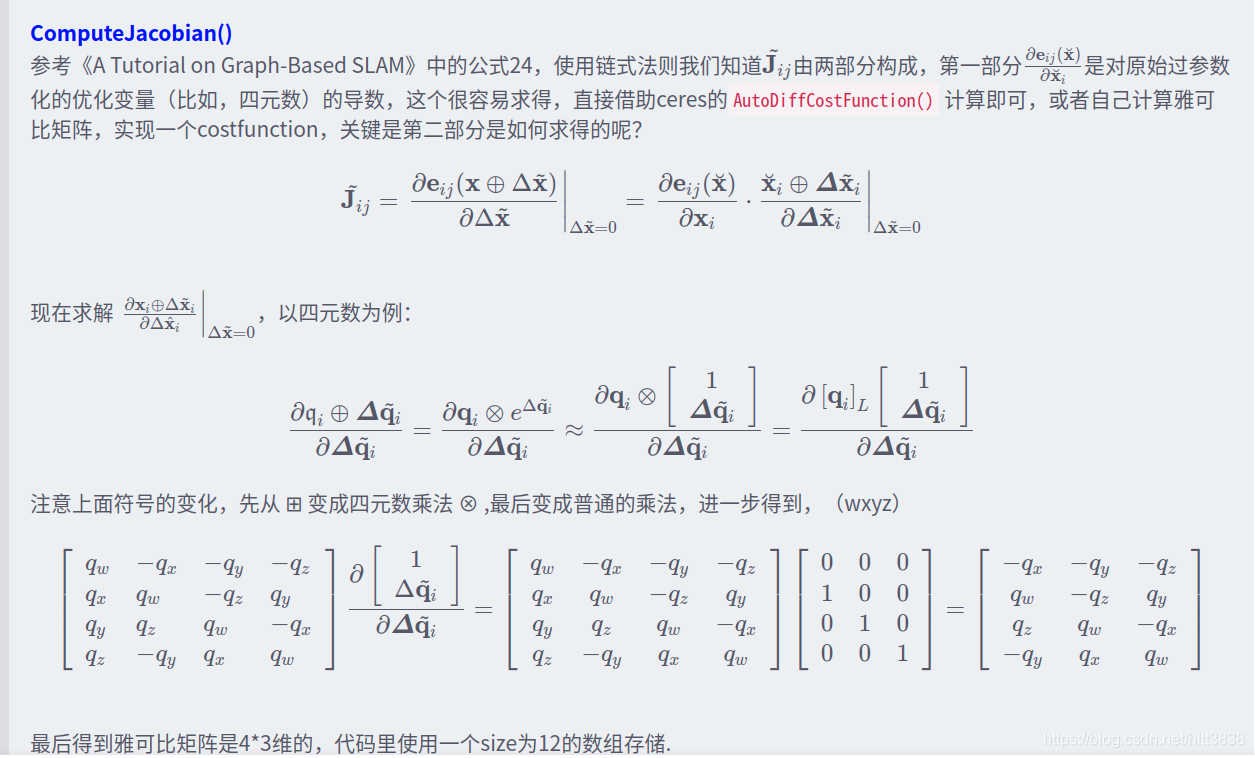
$r$ w.r.t $x_{L}$

在 ceres::CostFunction 处提供 residuals 对 Manifold 上变量的导数

\[J_{rG} = \frac{\partial r}{\partial x_G}\]

则对 Tangent Space 上变量的导数

\[J_{rL} = \frac{\partial r}{\partial x_L} = \frac{\partial r}{\partial x_G} \cdot J_{GL}\]

Sub Class

QuaternionParameterization
EigenQuaternionParameterization

自定义 QuaternionParameterization

参考 ⁷

Summary

QuaternionParameterization 的 Plus 与 ComputeJacobian 共同决定使用左扰动或使用右扰动形式

Quaternion in Eigen

Quaterniond q1(1, 2, 3, 4);           // wxyz
Quaterniond q2(Vector4d(1, 2, 3, 4)); // xyzw
Quaterniond q3(tmp_q);                // xyzw, double tmp_q[4];
q.coeffs();                           // xyzw