[TOC]

概述

SLAM，即 同时定位与建图，视觉SLAM的 定位 即 求取相机位姿（旋转和平移 $[\mathbf{R} \quad \mathbf{t}]$）；在SLAM中，我们一般使用 李代数 $\boldsymbol{\xi}$ 来表示 旋转和平移。

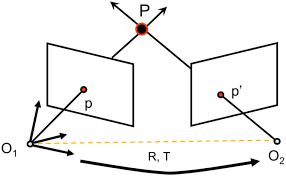
• 记 相机内参矩阵 $\mathbf{K}$，相机位姿 $\mathbf{T} = [\mathbf{R} \quad \mathbf{t}]$ (or $\boldsymbol{\xi}$)

• 记 $I_1$ 的图像坐标系下，一像素点 $\mathbf{p}(u,v)$；在 $O_1$ 相机坐标系下，其对应的 三维点 $\mathbf{P}(X,Y,Z)$

• 记 $I_2$ 的图像坐标系下，一像素点 $\mathbf{p’}(u’,v’)$；在 $O_2$ 相机坐标系下，其对应的 三维点 $\mathbf{P’}(X’,Y’,Z’)$，归一化坐标为$\mathbf{p’}_{norm}$

\[\mathbf{P'} = \mathbf{R} \cdot \mathbf{P} + \mathbf{t}\] \[\tilde{\mathbf{p'}}_{norm} = ({X'}_{norm},{Y'}_{norm},1) = \frac{\mathbf{P'}}{Z'} = (\frac{X'}{Z'}, \frac{Y'}{Z'}, 1)\] \[\tilde{\mathbf{p'}} = \mathbf{K} \cdot \tilde{\mathbf{p'}}_{norm}\]

在 优化位姿 时，其思想是构造一个关于位姿变化的误差函数，当这个误差函数最小时，认为此时估计的位姿最优。视觉SLAM主要分为 直接法 和 特征点法，但无论是直接法还是特征点法，位姿的迭代优化都是求解一个 最小二乘问题。

\[\min_{\boldsymbol{\xi}} \frac{1}{2} \left\| r(\boldsymbol{\xi}) \right\|^2\]

• 直接法 最小化 光度误差，即 前后帧像素的灰度误差

\[\begin{aligned} r(\boldsymbol{\xi}) &= \mathbf{I}_2(\mathbf{p}') - \mathbf{I}_1(\mathbf{p}) \\ &= \mathbf{I}_2(u',v') - \mathbf{I}_1(u,v) \end{aligned}\]

• 特征点法 最小化 重投影误差，即地图点到当前图像投影点与匹配点的坐标误差

\[\begin{aligned} r(\boldsymbol{\xi}) &= \mathbf{p}' - \mathbf{p} \\ &= (u',v') - (u,v) \end{aligned}\]

误差函数对于位姿的 雅可比矩阵(Jacobian Matrix)，决定着下一步最优迭代估计时 位姿增量的方向。

\[\mathbf{J}(\boldsymbol{\xi}) = \frac{\partial{r(\boldsymbol{\xi})}}{\partial \boldsymbol{\xi}}\]

根据上面位姿变换的流程，我们可以用 链式法则 来表示 $\mathbf{J}$

\[\begin{aligned} \mathbf{J}(\boldsymbol{\xi}) &= \frac{\partial{r(\boldsymbol{\xi})}}{\partial \boldsymbol{\xi}} \\ &= \frac{\partial{r(\boldsymbol{\xi})}}{\partial \mathbf{p}'} \cdot \frac{\partial \mathbf{p}'}{\partial \mathbf{p}_{norm}'} \cdot \frac{\partial \mathbf{p}_{norm}'}{\partial \mathbf{P'}} \cdot \frac{\partial \mathbf{P'}}{\partial \boldsymbol{\xi}} \\ &= \mathbf{J}_0 \cdot \mathbf{J}_1 \cdot \mathbf{J}_2 \cdot \mathbf{J}_3 \end{aligned}\]

由此，直接法 与 特征点法 雅克比矩阵 只区别于 $\mathbf{J}_0$。

本文主要介绍 SLAM优化位姿时误差函数对位姿雅可比矩阵的推导。

雅克比矩阵 推导

$J_0$

\[\mathbf{J}_0 = \frac{\partial{r(\boldsymbol{\xi})}}{\partial \mathbf{p}'}\]

直接法

我们已知， 在直接法中，单像素点的误差函数是关于像素值的函数，即 光度误差

\[r(\boldsymbol{\xi}) = \mathbf{I}_2(u',v') - \mathbf{I}_1(u,v)\]

由于对于一个特定的像素点，$\mathbf{I}_1(\mathbf{p})$ 是关于 $\boldsymbol{\xi}$ 的常量，所以

\[\begin{aligned} \mathbf{J}_0 &= \frac{\partial \mathbf{I}_2(\mathbf{p}')}{\partial \mathbf{p}'} \\ &= \bigg[ \frac{\mathbf{I}_2(u'+1,v')-\mathbf{I}_2(u'-1,v')}{2}, \frac{\mathbf{I}_2(u',v'+1)-\mathbf{I}_2(u',v'-1)}{2} \bigg] \end{aligned}\]

为 图像 $\mathbf{I}_2$ 在 $\mathbf{p}’$ 点处的 像素梯度

特征点法

我们已知， 在直接法中，单像素点的误差函数是关于像素坐标的函数

\[r(\boldsymbol{\xi}) = \mathbf{p}' - \mathbf{p}\]

由于对于一个特定的像素点，$\mathbf{p}$ 是关于 $\boldsymbol{\xi}$ 的常量，所以

\[\mathbf{J}_0 = \frac{\partial \mathbf{p}'}{\partial \mathbf{p}'} = \mathbf{I} \in \mathbb{R}^{2 \times 2}\]

$J_1$

\[\mathbf{J}_1 = \frac{\partial \mathbf{p}'}{\partial \mathbf{p}_{norm}'} = \frac{\partial (u,v)}{\partial (X_{norm}',Y_{norm}')}\]

由于

\[\tilde{\mathbf{p'}} = \mathbf{K} \cdot \tilde{\mathbf{p'}}_{norm}\]

$\mathbf{J}_1$ 的计算跟 相机投影模型 有关，本文以 针孔相机模型 （不考虑畸变）为例 对其进行计算。

针孔相机模型（不考虑畸变） 的 数学模型 为

\[\mathbf{K} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}\]

所以

\[\mathbf{J}_1 = \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \in \mathbb{R}^{2 \times 2}\]

$J_2$

\[\begin{aligned} \mathbf{J}_2 &= \frac{\partial \mathbf{p}_{norm}'}{\partial \mathbf{P'}} \\ &= \frac{\partial (X_{norm}',Y_{norm}')}{\partial (X',Y',Z')} \end{aligned}\]

根据

\[\tilde{\mathbf{p'}}_{norm} = \frac {\mathbf{P'}} {Z'}\]

计算得

\[\begin{aligned} \mathbf{J}_2 &= \begin{bmatrix} \frac{1}{Z'} & 0 & -\frac{X'}{Z'^2} \\ 0 & \frac{1}{Z'} & -\frac{Y'}{Z'^2} \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 & -\frac{X'}{Z'} \\ 0 & 1 & -\frac{Y'}{Z'} \end{bmatrix} \cdot \frac{1}{Z'} \in \mathbb{R}^{2 \times 3} \end{aligned}\]

$J_3$

使用 李代数

\[\begin{aligned} \mathbf{J}_3 &= \frac{\partial \mathbf{P'}}{\partial \boldsymbol{\xi}} \\ &= \frac{\partial (\mathbf{T} \cdot \mathbf{P})}{\partial \boldsymbol{\xi}} \\ &= \frac{\partial ( \exp(\boldsymbol{\xi}^{\wedge}) \mathbf{P}) }{\partial \boldsymbol{\xi}} \end{aligned}\]

其中

\[\boldsymbol{\xi} = \begin{bmatrix} \boldsymbol{\rho} \\ \boldsymbol{\phi} \end{bmatrix} \in \mathbb{R}^6\]

类似高数中，求取 $f(x)$ 的导数

\[\frac{df}{dx} = \lim_{\Delta x \rightarrow 0} \frac{f(x+\Delta x) - f(x)}{\Delta x}\]

我们可以 根据李代数加法来对李代数进行求导，计算雅克比矩阵。

一般更使用的，利用李群来左乘或者右乘微小扰动，在对这个扰动的李代数进行求导，利用 扰动模型 $\delta \boldsymbol{\xi} = [\delta \boldsymbol{\rho} \quad \delta \boldsymbol{\phi}]$，计算如下

\[\begin{aligned} \frac{\partial \tilde{\mathbf{P'}}}{\partial \boldsymbol{\xi}} &= \frac{\partial (\mathbf{T} \cdot \tilde{\mathbf{P}})}{\partial \boldsymbol{\xi}} \\ &= \frac{\partial ( \exp(\boldsymbol{\xi}^{\wedge}) \tilde{\mathbf{P}} ) }{\partial \delta \boldsymbol{\xi}} \quad \text{(左扰动模型)} \\ &= \lim_{\delta \boldsymbol{\xi} \rightarrow 0} \frac { \exp(\delta \boldsymbol{\xi}^{\wedge}) \exp(\boldsymbol{\xi}^{\wedge}) \tilde{\mathbf{P}} - \exp(\boldsymbol{\xi}^{\wedge}) \tilde{\mathbf{P}} } { \delta \boldsymbol{\xi} } \\ &\approx \lim_{\delta \boldsymbol{\xi} \rightarrow 0} \frac { (\mathbf{I}+ \delta \boldsymbol{\xi}^{\wedge}) \exp(\boldsymbol{\xi}^{\wedge}) \tilde{\mathbf{P}} - \exp(\boldsymbol{\xi}^{\wedge}) \tilde{\mathbf{P}} } { \delta \boldsymbol{\xi} } \\ &= \lim_{\delta \boldsymbol{\xi} \rightarrow 0} \frac { \delta \boldsymbol{\xi}^{\wedge} \exp(\boldsymbol{\xi}^{\wedge}) \tilde{\mathbf{P}} } { \delta \boldsymbol{\xi} } \\ &= \lim_{\delta \boldsymbol{\xi} \rightarrow 0} \frac { \begin{bmatrix} \delta \boldsymbol{\phi}^{\wedge} & \delta \boldsymbol{\rho} \\ \mathbf{0}^{T} & 0 \end{bmatrix} \begin{bmatrix} \mathbf{R} \cdot \mathbf{P} + \mathbf{t} \\ 1 \end{bmatrix} } { \delta \boldsymbol{\xi} } \\ &= \lim_{\delta \boldsymbol{\xi} \rightarrow 0} \frac { \begin{bmatrix} \delta \boldsymbol{\phi}^{\wedge} (\mathbf{R} \cdot \mathbf{P} + \mathbf{t}) + \delta \boldsymbol{\rho} \\ 0 \end{bmatrix} } { \delta \boldsymbol{\xi} } \\ &= \begin{bmatrix} \mathbf{I} & -(\mathbf{R} \cdot \mathbf{P} + \mathbf{t})^{\wedge} \\ \mathbf{0}^{T} & \mathbf{0}^{T} \end{bmatrix} \\ &= \begin{bmatrix} \mathbf{I} & -\mathbf{P}'^{\wedge} \\ \mathbf{0}^{T} & \mathbf{0}^{T} \end{bmatrix} \end{aligned}\]

所以

\[\begin{aligned} \mathbf{J}_3 &= \begin{bmatrix} \mathbf{I} & -\mathbf{P}'^{\wedge} \end{bmatrix} \\ &= \begin{bmatrix} 1 & 0 & 0 & 0 & Z' & -Y' \\ 0 & 1 & 0 & -Z' & 0 & X' \\ 0 & 0 & 1 & Y' & -X' & 0 \end{bmatrix} \in \mathbb{R}^{3 \times 6} \end{aligned}\]

注意：

• 上面的 $\boldsymbol{\xi}$ 中 平移 $\boldsymbol{\rho}$ 在前， 旋转 $\boldsymbol{\phi}$ 在后；如果 旋转在前，平移在后，则 $\mathbf{J}_3$ 的前三列与后三列须对调。

• ch4 为什么能用左扰动模型来求导啊？[gaoxiang12/slambook Issues #183]

  按照定义，左乘一个扰动，然后令扰动趋于零，求目标函数相对于扰动的变化率，作为导数来使用。同时，在优化过程中，用这种导数算出来的增量，以左乘形式更新在当前估计上，于是使估计值一直在SO(3)或SE(3)上。这种手段称为“流形上的优化”。

• 四元数矩阵与 so(3) 左右雅可比

使用 四元数

若旋转使用 四元数 表示，则更新小量为 $\begin{bmatrix} \delta \mathbf{t} \ \delta \boldsymbol{\theta} \end{bmatrix}$，则

\[\begin{aligned} \mathbf{J}_3 &= \frac{\partial \mathbf{P'}} {\partial \begin{bmatrix} \delta \mathbf{t} \\ \delta \boldsymbol{\theta} \end{bmatrix}} &= \frac{\partial (\mathbf{R} \cdot \mathbf{P} + \mathbf{t})} {\partial \begin{bmatrix} \delta \mathbf{t} \\ \delta \boldsymbol{\theta} \end{bmatrix}} &= \left[ \frac{\partial \mathbf{t}}{\partial \delta \mathbf{t}} \quad \frac{\partial (\mathbf{R} \cdot \mathbf{P})}{\partial \delta \boldsymbol{\theta}} \right] \end{aligned}\]

with

\[\begin{aligned} \frac{\partial (\mathbf{R} \cdot \mathbf{P})}{\partial \delta \boldsymbol{\theta}} &= \lim_{\delta \boldsymbol{\theta} \rightarrow 0} \frac {\exp(\delta \boldsymbol{\theta}^\wedge) \mathbf{R} \mathbf{P} - \mathbf{R} \mathbf{P}} {\delta \boldsymbol{\theta}} \\ &= \lim_{\delta \boldsymbol{\theta} \rightarrow 0} \frac {(\mathbf{I} + \delta \boldsymbol{\theta}^\wedge) \mathbf{R} \mathbf{P} - \mathbf{R} \mathbf{P}} {\delta \boldsymbol{\theta}} \\ &= \lim_{\delta \boldsymbol{\theta} \rightarrow 0} \frac {\delta \boldsymbol{\theta}^\wedge \mathbf{R} \mathbf{P}}{\delta \boldsymbol{\theta}} \\ &= -{(\mathbf{R} \cdot \mathbf{P})}^\wedge \end{aligned}\]

此时

\[\begin{aligned} \mathbf{J}_3 = \left[ \mathbf{I}_{3 \times 3} \quad -{(\mathbf{R} \cdot \mathbf{P})}^\wedge \right] \end{aligned}\]

总结

直接法

\[\begin{aligned} \mathbf{J}(\boldsymbol{\xi}) &= \mathbf{J}_0 \cdot \mathbf{J}_1 \cdot \mathbf{J}_2 \cdot \mathbf{J}_3 \\ &= \frac{\partial \mathbf{I}_2(\mathbf{p}')}{\partial \mathbf{p}'} \cdot \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -\frac{X'}{Z'} \\ 0 & 1 & -\frac{Y'}{Z'} \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 & Z' & -Y' \\ 0 & 1 & 0 & -Z' & 0 & X' \\ 0 & 0 & 1 & Y' & -X' & 0 \end{bmatrix} \cdot \frac{1}{Z'} \end{aligned}\]

特征点法

• 使用 李代数

\[\begin{aligned} \mathbf{J}(\boldsymbol{\xi}) &= \mathbf{J}_0 \cdot \mathbf{J}_1 \cdot \mathbf{J}_2 \cdot \mathbf{J}_3 \\ &= \mathbf{I} \cdot \begin{bmatrix} f_x & 0 \\ 0 & f_y \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & -\frac{X'}{Z'} \\ 0 & 1 & -\frac{Y'}{Z'} \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 & Z' & -Y' \\ 0 & 1 & 0 & -Z' & 0 & X' \\ 0 & 0 & 1 & Y' & -X' & 0 \end{bmatrix} \cdot \frac{1}{Z'} \\ &= \begin{bmatrix} \frac{f_x}{Z'} & 0 & -\frac{X'f_x}{Z'^2} \\ 0 & \frac{f_y}{Z'} & -\frac{Y'f_y}{Z'^2} \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 & 0 & Z' & -Y' \\ 0 & 1 & 0 & -Z' & 0 & X' \\ 0 & 0 & 1 & Y' & -X' & 0 \end{bmatrix} \\ &= \begin{bmatrix} \frac{f_x}{Z'} & 0 & -\frac{X'f_x}{Z'^2} & -\frac{X'Y'f_x}{Z'^2} & f_x+\frac{X'^2f_x}{Z'^2} & -\frac{Y'f_x}{Z'} \\ 0 & \frac{f_y}{Z'} & -\frac{Y'f_y}{Z'^2} & -f_y-\frac{Y'^2f_y}{Z'^2} & \frac{X'Y'f_y}{Z'^2} & \frac{X'f_y}{Z'} \end{bmatrix} \end{aligned}\]

• 使用 四元数

\[\mathbf{J} = \begin{bmatrix} \frac{f_x}{Z'} & 0 & -\frac{X'f_x}{Z'^2} \\ 0 & \frac{f_y}{Z'} & -\frac{Y'f_y}{Z'^2} \end{bmatrix} \cdot \left[ \mathbf{I}_{3 \times 3} \quad -{(\mathbf{R} \cdot \mathbf{P})}^\wedge \right]\]

注意事项

• $\mathbf{J}_1$ 的计算是根据 针孔相机模型（不考虑畸变） 进行计算的
• 本文的 $\boldsymbol{\xi}$ 中 平移 $\boldsymbol{\rho}$ 在前， 旋转 $\boldsymbol{\phi}$ 在后；如果 旋转在前，平移在后，则 $\mathbf{J}_3$ 的前三列与后三列须对调
• 本文定义的 误差函数 $r(\boldsymbol{\xi})$ 为 预测值减观测值；如果定义成 观测值减预测值，本文计算的结果 $\mathbf{J}$ 前须加 负号

参考文献

• SLAM优化位姿时，误差函数的雅可比矩阵的推导

• 《视觉SLAM十四讲》