[TOC]
Overview
-
一般表示形式
-
优化形式(避免过参数化)
特征的参数化表示,即以何种方式表示特征,在优化中决定了特征以何种参数进行的迭代更新,或者 在EKF中决定了以何种参数构建高斯模型。不论在优化还是EKF中,我们关心的都是特征在图像上的投影与特征参数之间的关系(Jacobian)。
过参数化(Overparameterization) 问题
特征参数化之后参数的个数大于实际表示的 自由度 的表现形式就被称为 过参数化
3D Point
\[P: \left[ X \; Y \; Z \right]^T\]- 3 DoF
ref:
XYZ
- Global XYZ
- Anchored XYZ
Inverse Depth
- Global inverse depth (spherical coordinates)
- has a singularity when the z-distance goes to zero
- 球坐标逆深度仅在xyz都趋近于0时才存在数值奇异,所以能用在全局坐标系
- Anchored inverse depth (MSCKF)
- 逆深度 + normalized UV (Bearing Vector)
- Anchored inverse depth (MSCKF single depth)
- 逆深度
- the the single depth from VINS-Mono
3D Line
\[L: \left[ P_0 \; P_1 \right]\]- 4 DoF
ref:
普吕克(Plucker)坐标
- 过参数化 问题
正交表示法
3D Plane
\[Ax + By + Cz + D = 0\]- 3 DoF
ref:
Hesse
用一个平面的 单位法向量 和 平面距离原点的 距离 来表示
\[\pi: \left(\mathbf{n}^{\top}, d\right)^{\top} \in \mathbb{R}^4\]过参数化 问题:平面的Hesse形式的过参数化就是因为单位法向量部分有3个参数,但是实际只有两个自由度导致的。
球坐标
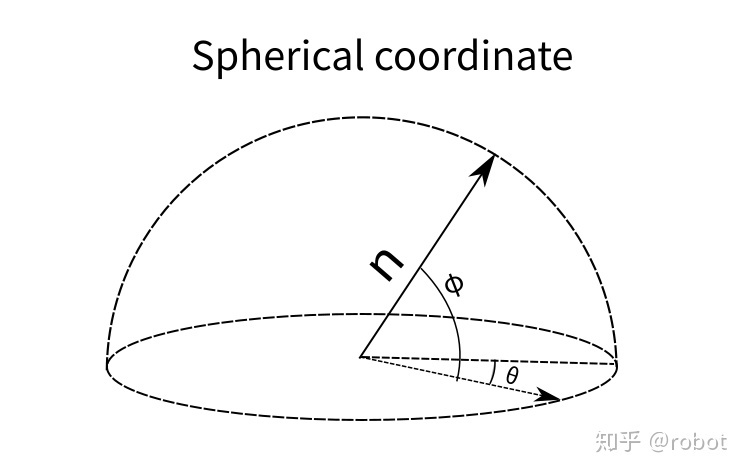
单位法向量可以被看成是一个单位圆球上的一点,那么就可以用两个角度 $\theta$ 和 $\phi$ 来参数化这个点,从而表示出这个单位法向量。
\[\pi: \left[ \theta \; \phi \; d \right] \in \mathbb{R}^3\] \[\tau=(\theta, \phi, d)^{\top}= q(\pi)=\left(\theta=\arctan \frac{n_{y}}{n_{x}}, \; \phi=\arcsin n_{z}, \; d\right)^{\top}\]切平面
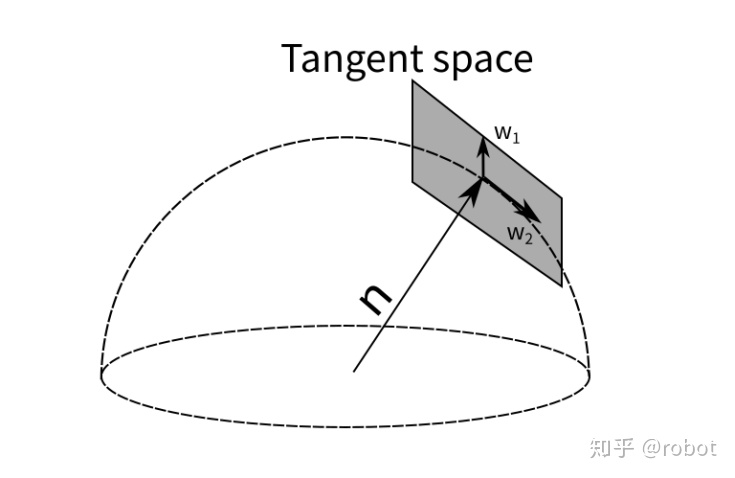
GTSAM里面表示面的方式用切平面的方式来更新单位法向量,同样也可以被用来优化单位法向量。
最近点
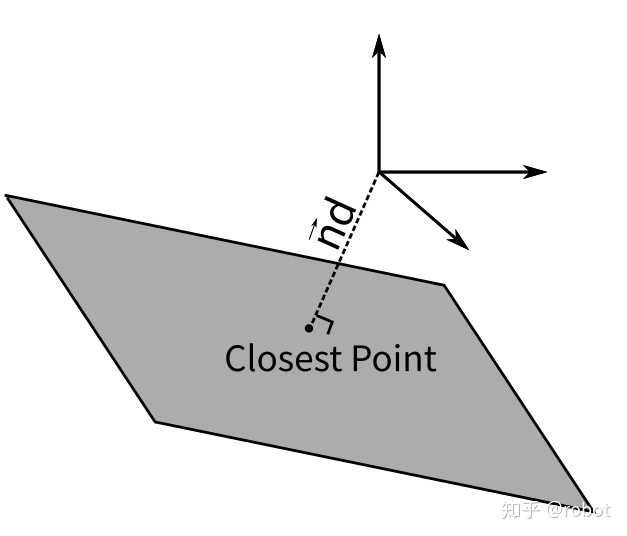
单位四元数
退化二次曲面 1
Unified Representation
- paper 1

PREVIOUS图像频率域分析之频域谱(FDE)