CG-SpatialAI

Mesh Texturing in a Nutshell (Let There Be Color)

 
  • Jun 12, 2022
  • 0 views

[TOC]

Overview

digraph {
  TV [label="TextureView"];
  TVs [label="N TextureViews"];
  Texturing [style=filled, shape=box];
  ColorImg->TV;
  CamK->TV;
  CamTF->TV;
  TV->TVs;
  TVs->Input;
  TriangleMesh->Input;
  Input->Texturing->Output->TexturedMesh;
}
  • code (forked): https://github.com/cggos/mvs-texturing
  • paper: Let There Be Color! Large-Scale Texturing of 3D Reconstructions
  • video: https://www.youtube.com/watch?v=Ie-qLJdmlLI

1. Texture Views

tex::generate_texture_views()

digraph {
  TV [label="TextureView"];
  TV->ColorImg;
  TV->CamK;
  TV->CamTF;
}

2. Mesh –> MeshInfo

tex::prepare_mesh()

Check Mesh

TriangleMesh::ensure_normals()
  • Ensure face and vertex normals

Init MeshInfo 

MeshInfo::initialize()

Create VertexInfo

Add faces to their three vertices

digraph {
  vertex -> face1
  vertex -> face2
  vertex -> face3
}

Update VertexInfo

Classify each vertex and compute adjacenty info

  • Build new, temporary adjacent faces representation AdjacentFaceList adj_temp for ordering
digraph {
  face_id [color=green];
  front_vid [color=blue];
  back_vid [color=blue];

  AdjFaceTmp->face_id
  AdjFaceTmp->front_vid
  AdjFaceTmp->back_vid
}

graph {
  layout=twopi;
  node [shape=circle];

  v0 [color="red"];
  v1 [color="blue"];
  v2 [color="blue"];

  v0--v1 [color=green];
  v0--v2 [color=green];
  v0--v3;
  v0--v4;
  v1--v2 [color=green];
  v3--v2;
  v3--v4;
  v1--v4;

  overlap=false;
}

  • Sort adjacent faces by chaining them

    AdjacentFaceList adj_sorted;

  • update VertexInfo

digraph {
  vclass;
  verts [color=blue];
  faces [color=green];

  vinfo->vclass;
  vinfo->verts;
  vinfo->faces;
}

3. Mesh + MeshInfo –> Adjacency Graph (UniGraph)

tex::build_adjacency_graph()

对于每个 face，将mesh中与其每条 edge 邻接的 face 存入 adj_faces；将当前 face 与 adj_faces 中每个 face 建立 edge，构建 UniGraph 。

graph {
  node [shape=circle];

  f0--f1; f1--f2;
  f0--f3; f3--f4;
  f1--f4;

  overlap=false;
}

4. View Selection –> Best View Label :smile: 

tex::calculate_data_costs()

tex::view_selection()

Calculate DataCosts

Calculates the data costs for each face and texture view combination, if the face is visible within the texture view.

FaceProjectionInfos face_projection_infos(num_faces);
calculate_face_projection_infos(mesh, texture_views, settings, &face_projection_infos);
postprocess_face_infos(settings, &face_projection_infos, data_costs);

Calculate FaceProjectionInfo 

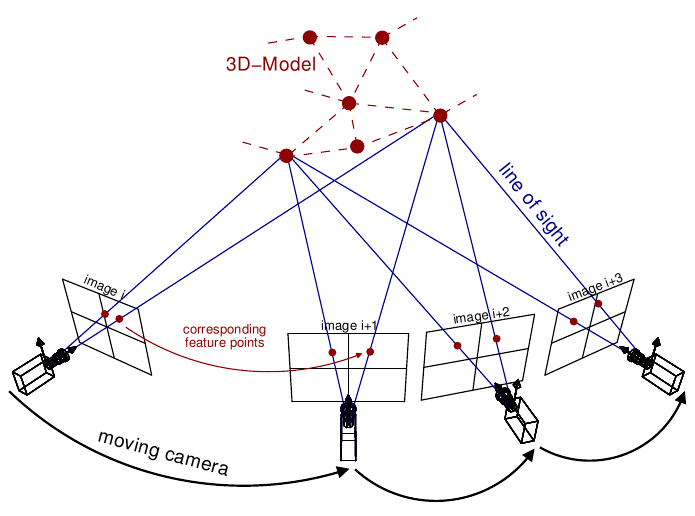
for (std::uint16_t j = 0; j < static_cast<std::uint16_t>(num_views); ++j) {
  TextureView * texture_view = &texture_views->at(j);
  // get view_pos and view_dir
  for (std::size_t i = 0; i < faces.size(); i += 3) {
    // get face_normal and face_center
    // compute and check viewing_angle
    // get face info
  }
}

digraph {
  face_info [style=filled];
  nnn [label="..."];
  face_info_n [style=filled];
  rankdir=LR;
  face_id->face_info;
  face_info->view_id;
  face_info->mean_color;
  face_info->quality;
  face_id->nnn;
  face_id->face_info_n;
}

PostProcess Face Infos

create hist_qualities::Histogram using info.quality, and get the upper_bound when percentile=0.995

compute data cost

  • gmi
  • area
float normalized_quality = std::min(1.0f, info.quality / percentile);
float data_cost = (1.0f - normalized_quality);
data_costs->set_value(i, info.view_id, data_cost);
DataCost face0 face1 … faceN
view0        
view1        
…        
viewN        

View Selection

Data Association

Graph mapmap::Graph<cost_t> 

graph {
  rankdir = LR;
  face_id--adj_face_id [label="weight"];
}

LabelSet mapmap::LabelSet<cost_t, simd_w>

view id face0 face1 … faceN
view0        
view1        
…        
viewN        

Unaries

using unary_t = mapmap::UnaryTable<cost_t, simd_w>;
std::vector<unary_t> unaries;
  face_id label_set costs
unary0      
unary1      
…      
unaryN      

Pairwise

using pairwise_t = mapmap::PairwisePotts<cost_t, simd_w>;
pairwise_t pairwise(1.0f);

MAP-MRF :triangular_flag_on_post: 

mapmap::mapMAP<cost_t, simd_w> solver;
solver.set_graph(&mgraph);
solver.set_label_set(&label_set);
for(std::size_t i = 0; i < graph->num_nodes(); ++i)
    solver.set_unary(i, &unaries[i]);
solver.set_pairwise(&pairwise);
solver.set_logging_callback(display);
solver.set_termination_criterion(&terminate);
solver.optimize(solution, ctr);

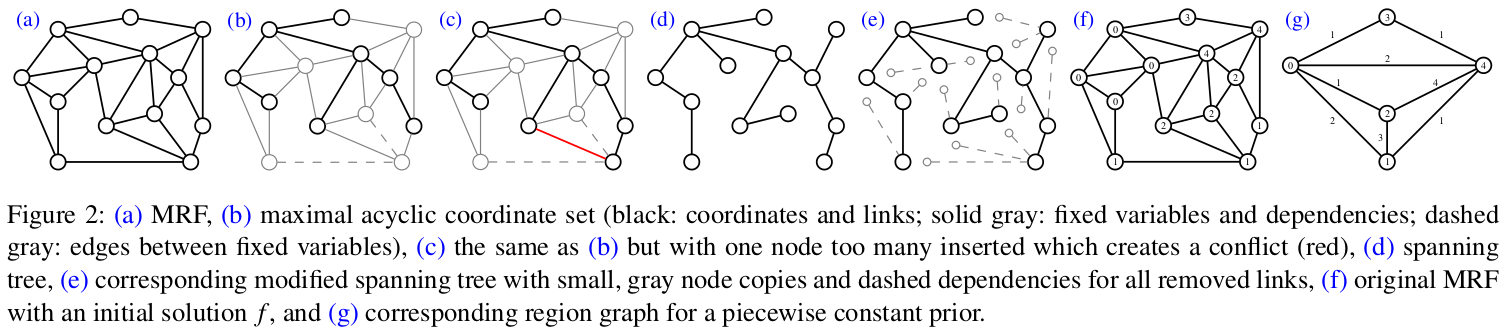
The aim is to find a labeling for X that produces the lowest energy.

pairwise MRFs

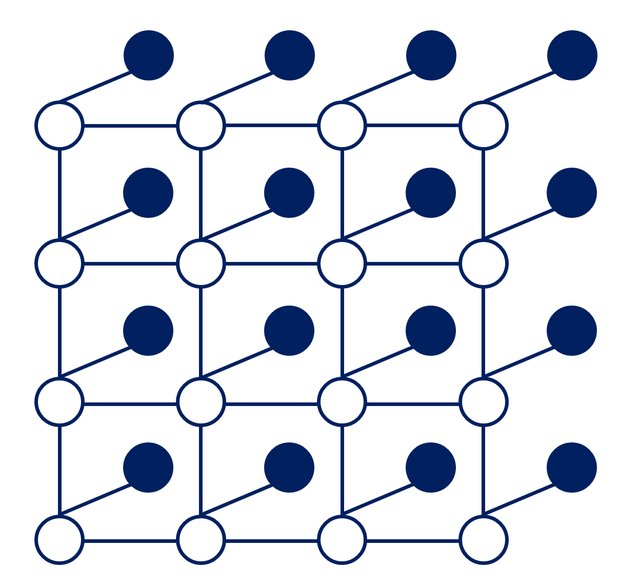
  • the filled-in circles: the observed nodes $Y_i$ (face)
  • the empty circles: the “hidden” nodes $X_i$ (view label)

MAP –> Minimum Energy

energy/cost function:

\[\text{energy} (Y, X) = \sum_{i} \text{DataCost} (y_i, x_i) + \sum_{j = \text{neighbours of i}} \text{SmoothnessCost} (x_i, x_j)\]
Tree MRFs via DP

LBP

by OpenMVS

5. Create Texture Atlases :smile: 

tex::generate_texture_patches()

tex::global_seam_leveling()
tex::local_seam_leveling()

tex::generate_texture_atlases()

Generate Texture Patches

Generates texture patches using the graph to determine adjacent faces with the same label.

Global / Local Seam Levelling :triangular_flag_on_post:

  • paper: Seamless Mosaicing of Image-Based Texture Maps

without seam levelling

Texture Atlases

generate TextureAtlas from all of TexturePatch

6. Mesh + Texture –> Obj Model

tex::build_model()

tex::Model::save()
  • .obj
  • .mtl
  • .png

网格UV展开

上述纹理重建属于 计算机视觉 的内容，本节是其逆过程，属于 计算机图形学 的内容。

  • http://geometryhub.net/notes/uvunfold

Reference

Search