[TOC]
Overview
三维空间中的变换主要分为如下几种:
- 射影变换
- 仿射变换
- 相似变换
- 欧式变换
其性质如下图所示:
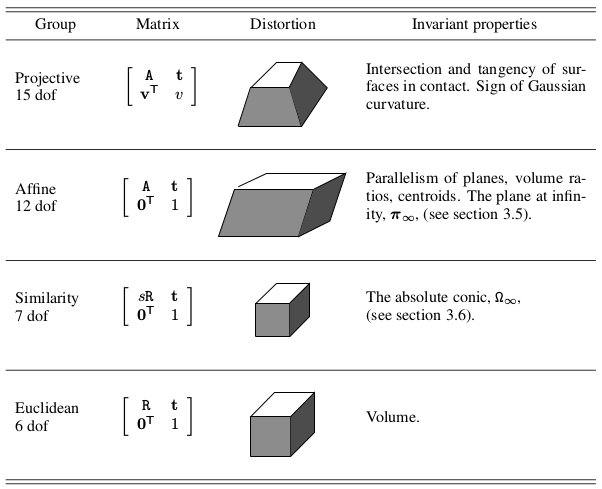
本文主要介绍欧式变换。
欧式变换
\[\mathbf{T} = \begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0}^T & 1 \end{bmatrix} \in \mathbb{R}^{4 \times 4}\] \[\mathbf{T}^{-1} = \begin{bmatrix} \mathbf{R}^T & -\mathbf{R}^T \cdot \mathbf{t} \\ \mathbf{0}^T & 1 \end{bmatrix} \in \mathbb{R}^{4 \times 4}\]Translate by $-C$ (align origins), Rotate to align axes:
\[\begin{aligned} P_c &= \mathbf{T} \cdot P_w \\ &= \mathbf{R} \cdot (P_w - C) \\ &= \mathbf{R} \cdot P_w - \mathbf{R} \cdot C \\ &= \mathbf{R} \cdot P_w + \mathbf{t} \end{aligned}\]坐标系手性
坐标系的手性主要分为 右手系 和 左手系,主要通过以下两种方法区分(右手系):
-
3 finger method
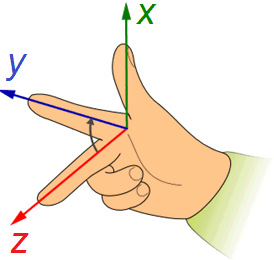
-
Curling method
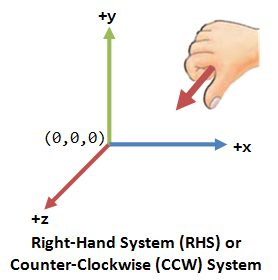
另外,不同的几何编程库所基于的坐标系的手性会有所不同
- Eigen: 右手系
- OpenGL: 右手系
- Unity3D: 左手系
- ROS tf: 右手系
注意事项
区分 点的变换 和 坐标系本身的变换
\[P_a = \mathbf{T}_{AB} \cdot P_b\]指的是 将某点在B坐标系中的坐标表示变换为其在A坐标系中的坐标表示,实质是同一点在不同坐标系下的不同坐标表示,即 点的变换;若将A和B坐标系假设为刚体,则B坐标系变换到A坐标系(坐标系本身的变换)的变换矩阵为 $\mathbf{T}_{AB}^{-1}$。
-
使用传感器(Camera-IMU)标定工具(例如Kalibr)标定出的外参指的是 点的变换
-
ROS中 static_transform_publisher 则是 坐标系本身的变换
static_transform_publisher x y z yaw pitch roll frame_id child_frame_id period_in_ms
在分析多个坐标系的姿态变换时,要注意根据点的变换或者坐标系的变换确定矩阵左乘还是右乘:
- 点的变换:矩阵相乘 从右到左,即 矩阵左乘
- 坐标系的变换:矩阵相乘 从左到右,即 矩阵右乘
区分 绕定轴旋转 和 绕动轴旋转
注意 右手系 和 左手系
编程库实践
下面通过示例代码对自己使用过的库进行介绍。
Eigen
Eigen is a C++ template library for linear algebra: matrices, vectors, numerical solvers, and related algorithms.
Eigen::Matrix3d m3_r_z = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();
Eigen::Quaterniond q_r_z(m3_r_z);
Eigen::Vector3f v3_translation(x, y, z);
Eigen::Quaternion<double> q(w, qx, qy, qz);
Eigen::Matrix3f m3_rotation = q.matrix();
Eigen::Matrix4f m4_transform = Eigen::Matrix4f::Identity();
m4_transform.block<3,1>(0,3) = v3_translation;
m4_transform.block<3,3>(0,0) = m3_rotation;
TooN
Tom’s Object-oriented numerics library, is a set of C++ header files which provide basic linear algebra facilities
#include <TooN/TooN.h>
#include <TooN/se3.h>
/**
* @brief transform array to TooN::SE3
* @param array array of 3x4 row-major matrix of RT
* @param se3 TooN::SE3 object
*/
void Tools::Array2SE3(const float *array, SE3<> &se3)
{
Matrix<3,3> m3Rotation;
for(int i=0;i<3;i++)
{
for(int j=0;j<3;j++)
{
m3Rotation[i][j] = array[i*4+j];
}
}
SO3<> so3 = SO3<>(m3Rotation);
Vector<3> v3Translation;
v3Translation[0] = array[ 3];
v3Translation[1] = array[ 7];
v3Translation[2] = array[11];
se3.get_rotation() = so3;
se3.get_translation() = v3Translation;
}
Sophus
C++ implementation of Lie Groups using Eigen commonly used for 2d and 3d geometric problems (i.e. for Computer Vision or Robotics applications)
#include <iostream>
#include <sophus/se3.hpp>
Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();
Eigen::Quaterniond q(R);
Eigen::Vector3d t(1,0,0);
Sophus::SE3 SE3_Rt(R, t);
Sophus::SE3 SE3_qt(q, t);
typedef Eigen::Matrix<double,6,1> Vector6d;
Vector6d se3 = SE3_Rt.log();
std::cout << "se3 hat = " << std::endl
<< Sophus::SE3::hat(se3) << std::endl;
std::cout <<"se3 hat vee = " << std::endl
<< Sophus::SE3::vee( Sophus::SE3::hat(se3) ).transpose() << std::endl;
Vector6d update_se3;
update_se3.setZero();
update_se3(0,0) = 1e-4d;
Sophus::SE3 SE3_updated = Sophus::SE3::exp(update_se3) * SE3_Rt;
std::cout << "SE3 updated = " << std::endl
<< SE3_updated.matrix() << std::endl;
ROS tf & tf2
tf is a package that lets the user keep track of multiple coordinate frames over time. tf maintains the relationship between coordinate frames in a tree structure buffered in time, and lets the user transform points, vectors, etc between any two coordinate frames at any desired point in time.
#include <Eigen/Geometry>
#include <tf_conversions/tf_eigen.h>
#include <tf2/LinearMath/Quaternion.h>
#include <tf2/LinearMath/Matrix3x3.h>
#include <geometry_msgs/TransformStamped.h>
tf::Transform transform;
transform.setOrigin( tf::Vector3(x, y, z) );
tf::Quaternion q;
q.setRPY(r, p, y);
transform.setRotation(q);
geometry_msgs::Quaternion q_msg;
Eigen::Vector3d v3_r;
tf2::Matrix3x3(tf2::Quaternion(q_msg.x, q_msg.y, q_msg.z, quaternion_imu_.w))
.getRPY(v3_r[0], v3_r[1], v3_r[2]);
tf2::Quaternion q_tf2;
q_tf2.setRPY(v3_r[0], v3_r[1], v3_r[2]);
q_tf2.normalize();
geometry_msgs::TransformStamped tf_stamped;
tf_stamped.transform.rotation.x = q.x();
tf_stamped.transform.rotation.y = q.y();
tf_stamped.transform.rotation.z = q.z();
tf_stamped.transform.rotation.w = q.w();